This website presents a SLAM evaluation toolkit developed at the University of Freiburg, Department of Computer Science.
We provide sets of relative relations needed to compute our metric for an extensive set of datasets frequently used in the robotics community. The relations have been obtained by manually matching laser-range observations to avoid the errors caused by matching algorithms. Our benchmark framework allows the user an easy analysis and objective comparisons between different SLAM approaches.
Description:
We address the problem of creating an objective benchmark for evaluating SLAM approaches. We propose a framework for analyzing the results of a SLAM approach based on a metric for measuring the error of the corrected trajectory. This metric uses only relative relations between poses and does not rely on a global reference frame. This overcomes serious shortcomings of approaches using a global reference frame to compute the error. Our method furthermore allows to compare SLAM approaches that use different estimation techniques or different sensor modalities since all computations are made based on the corrected trajectory of the robot.We propose to use a measure based on the relative displacement between poses to perform comparisons:
Close-to-ground-truth relations can be created by using manually aligned scans and relations introduced by hand (since the human knows the structure of the environment) or e.g. relations obtained from aerial images (in an outdoor setting).
The following images are an example of the performance measure on maps generated using different sensor setups. The long dashed line represents a relation added by manually measuring the relative distance at two locations of the robot:
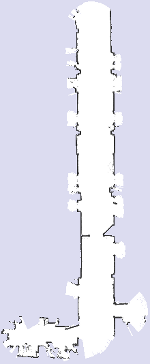 |
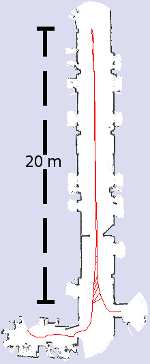 |
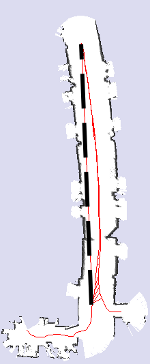 |
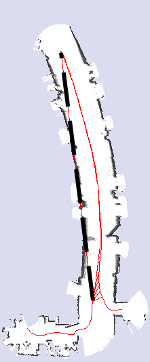 |
| (a) | (b) | (c) | (d) |
(b) The reference map superimposed with the network of relative measurements.
(c) A map obtained by scan matching using a 4 meters range sensor, with the superimposed relation.
(d) A map obtained by cropping the range of the sensor to 3 meters.
Whereas the quality of the rightmost map is visibly decreased, it is also adequate for robot navigation since it preserves a correct topology of the environment (all doorways are still visible) and it correctly reflects the local metric structure of the corridor.
The following figure shows the behavior of the error metric for the maps (c) and (d) in the figure above.
(Please note the logarithmic scale)
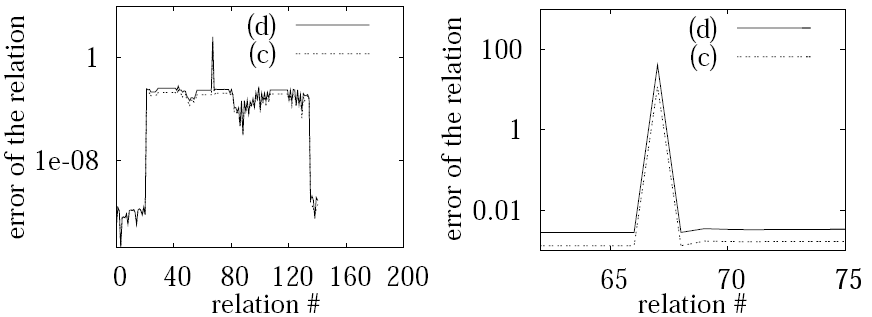
Left: The error introduced by the individual relations.
Right: Magnificiation of the region corresponding to the manually introduced relations marked on the map images with the dashed line.
Publications
For more details or if you want to cite our work, please refer to the following papers:On Measuring the Accuracy of SLAM Algorithms by Rainer Kümmerle, Bastian Steder, Christian Dornhege, Michael Ruhnke, Giorgio Grisetti, Cyrill Stachniss, and Alexander Kleiner
Journal of Autonomous Robots, 27(4):387-407, 2009.
Online Version
A Comparison of SLAM Algorithms Based on a Graph of Relations by W. Burgard, C. Stachniss, G. Grisetti, B. Steder, R. Kümmerle, C. Dornhege, M. Ruhnke, A. Kleiner, and Juan D. Tardós.
In Proc. of the IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS). St. Louis, MO, USA, October 2009.